Notions d'apprentissage

Nous avons vu au chapitre précédent que nous parlons d'apprentissage pour les techniques supervisées vs non supervisées.

Toutefois, la littérature se réfère davantage aux techniques supervisées pour évoquer les principes d'apprentissage. Cela a une certaine logique étant donné que dans le cadre de l'application d'une technique supervisée, nous, en tant que data scientist, jouons le rôle de professeur de la machine et dans cette démarche, nous l'entrainons et nous vérifions si la machine a bien appris ; c'est à dire si elle fait correctement son travail. A contrario, les techniques non-supervisées ne sont pas explicitement guidées dans l'apprentissage qui est entièrement autonome à la machine et dont la finalité sera de mettre en avant des tendances ou des relations cachées que nous en tant que data scientist devront interpréter comme étant utile ou non.

D'ailleurs un autre élément fondamental qui distincte un apprentissage supervisé d'un apprentissage non-supervisé est le fait que la machine, dans un apprentissage supervisé, assurera une continuité de cet apprentissage de manière autonome par la suite. Nous avons vu comme exemple que si nous apprenons à une machine que lorsqu'un email contient les mots « gratuit », « loterie » et « argent », il y a une forte probabilité que ce soit un spam ( courrier non désirable ), la machine pourrait découvrir par la suite que le mot « bitcoin » est souvent reprit également avec ces mots et donc sans que nous l'ayons explicitement programmée, elle intégrera une nouvelle règle : celle d'identifier le mot « bitcoin » comme ayant une certaine probabilité à être un spam. Dans le cadre d'un apprentissage non-supervisé, à chaque fois que l'on applique l'algorithme sur des nouvelles données, on obtiendra un nouveau modèle, c'est à dire que la machine recommencera son apprentissage à zéro.

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

Déroulement d'un apprentissage supervisé

Pour réaliser un modèle de prédiction, nous devons disposer de données qui comprennent les valeurs que l’on souhaite prédire. On parle de données « étiquetées » ( labeled data ). Nous devons donc disposer de colonnes considérées comme étant des variables explicatives ( des prédicteurs, les X : X₁, X₂,X₃,... ) ainsi qu'une variable à expliquer (l a variable prédite Y ).

Répartition d'un dataframe en variables explicatives et variable cible

La première étape d'un apprentissage supervisés et donc d'identifier et sélectionner les X et également identifier la colonne Y. Bien entendu, nous partons de l'hypothèse que nous disposons de données « propres », c'est à dire que toutes les étapes d'analyse ( analyse statistique univariée ) et de préparation ( notamment des transformations ingénierie des caractéristiques ) ont été réalisées et les données sont structurées et donc représentées sous forme tabulaire. Nous partons également du postulat que la sélection des prédicteurs - variables explicatives les plus utiles pour créer notre modèle - a déjà été réalisé également.

Nous disposons d'une table contenant des colonnes X et une colonne Y, comme suit :

X₁	X₂	X₃	X_...	X_n	Y
X_1,1	X_1,2	X_1,3	...	X_1,n	Y₁
X_2,1	X_2,2	X_2,3	...	X_n,n	Y₂
...	...	...	...	...	...
X_n,1	X_n,2	X_n,3	...	X_n,n	Y₃

astuce

X_2,3 correspond à la valeur de la 2e ligne de la 3e colonne

Pour convertir nos données en X et Y, il suffit simplement de donner l'instruction des colonnes appartenant à X et celle appartenant à Y. L'écriture [['En-tête Colonne 1','En-tête Colonne 2' ]] signifie qu'il y a plusieurs colonnes, alors que [ ] signifie qu'il n'y a qu'une seule colonne.

import pandas as pd

df = pd.DataFrame(data)

X = df[['X1', 'X2', 'X3']]  
y = df['Y']

Partitionnement des données

La seconde étape consiste à subdiviser ( partitionner ) les enregistrements afin d'utiliser une partition pour créer le modèle ( apprendre à la machine ) et l'autre partition pour valider le modèle ( vérifier que l'élève, la machine, a bien appris ).

On partitionne donc les enregistrements des colonnes X et Y en deux parties :

Set d'entrainement qui comprends les données d'apprentissage
Set de test qui comprends les données qui seront utilisées pour vérifier l'apprentissage

Le partitionnement des données ( aléatoire ) dépend fortement de la quantité de données à disposition et de la complexité des techniques qui seront utilisées. Par exemple, si on dispose d'un nombre de données restreint, le partitionnement sera réalisé comme suit : Set d'entrainement $60 %$ ; Set de test $40 %$ .

Par contre, si on dispose de nombreuse données et que la technique requière un nombre important d'enregistrements ( par exemple un réseau de neurones ), le partitionnement sera réalisé comme suit : Set d'entrainement $80 %$ ; Set de test $20 %$ .

💡 Tip: La répartition des enregistrements entre la partition « entrainement » et la partition « test » doit être réalisée de manière aléatoire

Ce partitionnement peut être réalisé de manière simple à l'aide de la librairie spécialisée en machine learning : sickit-learn :

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = 
  train_test_split(X, y, test_size=0.2, random_state=42)

X et y reprennent toutes nos données. X contient plusieurs colonnes et de nombreux enregistrements. Y ne contient qu'une colonne et le même nombre d'enregistrements que X. La fonction train_test_split va nous permettre de réaliser ce partitionnement et comprends ci-dessus 4 arguments. Le premier identifie les X, le second identifie y, le troisième définit la taille de la partition de test ( dans ce cas-ci 20 % ) et le quatrième paramètre, random_state, permet de définir un point de départ fixe pour le processus aléatoire. Cela garantit que chaque fois que nous exécutons la fonction train_test_split avec la même valeur pour random_state (par exemple 42), nous obtiendrons exactement la même division des données.

Étape d'apprentissage

Dans la phase d'apprentissage, nous appliquons une technique statistique à nos données d'entrainement. Par exemple, pour la régression linéaire, technique supervisée paramétrique, l'algorithme va réaliser un processus comprenant différentes étapes permettant de définir les paramètres, c'est à dire les incidences des valeurs de X sur la valeur Y. Par exemple : l'incidence de la superficie en m² d'une maison sur sa valeur.

L'algorithme - qui consiste en une série d'étapes ( y compris l'étape de partitionnement des données ) - , va nous fournir un modèle que nous allons pouvoir appliquer à de nouvelles données.

Voici un exemple d'apprentissage en appliquant un modèle de régression linéaire prédéfini ( Nous décomposerons ce modèle dans le chapitre sur la régression linéaire ).

model = LinearRegression()
model.fit(X_train, y_train)

Étape de validation

Dès que nous obtenons un modèle, nous allons le vérifier, c'est à dire le valider. La manière la plus simple de réaliser une première validation est de vérifier si le modèle fonctionne correctement en lui appliquant les données sur base desquelles il a réalisé son apprentissage, mais cette fois-ci, on va lui cacher les valeurs des y et lui demander de les prédire. Étant donné que nous utilisons les mêmes données que celle utilisées lors de l'apprentissage, nous nous attendons à obtenir à cette étape-ci, un excellent score en vérifiant les valeurs prédites par rapport aux valeurs réelles. L'idée est de s'assurer que ce modèle est robuste dans son apprentissage.

y_pred = model.predict(X_train)

Nous utilisons la fonction de prédiction de notre modèle sur les mêmes valeurs de X à partir desquelles notre modèle a été créé.

Les erreurs de prédiction dans le set d’entrainement ( validation ) nous donnent une indication sur l’ajustement du modèle ( sous-entraîné ou surentrainé ).

attention

L'erreur dans l'étape de validation, c'es à dire la différence entre les valeurs prédites et valeurs réelles doit être minimale mais ne doit absolument pas correspondre à 0. Si vous obtenez 0, c'est que votre modèle est en sur-apprentissage. Il connait trop bien ses données d'entrainement et ne sera probablement pas généralisable et donc donnera un score médiocre sur de nouvelles données ( par exemple lors de l'étape de test )

Étape de test

Si l'étape de validation est concluante, c'est à dire que nous obtenons une fiabilité élevée ( faible différence entre les valeurs prédites par le modèle et les valeurs réelles connues ), nous passons à la phase de test. Attention, si l'étape de validation mène à une fiabilité faible, cela signifie que le modèle est sous-entrainé. Il n'est pas capable de prédire correctement des valeurs sur lesquelles il a été entrainé ! Il ne dispose pas de suffisamment d'enregistrements ou de colonnes et d'enregistrements.

L'étape de test consiste à appliquer notre modèle sur la seconde partition de nos données, celles à partir desquelles notre modèle n'a pas été entrainé mais dont nous connaissons les valeurs des X et les valeurs des Y. Nous appliquons la fonction de prédiction sur les X et nous comparons les valeurs des Y obtenues.

y_pred = model.predict(X_test)

Nous vérifions ensuite la différence entre les valeurs prédites et les valeurs réelles.

Le résultat de l'étape de test devrait être légèrement inférieur à l'étape de validation signifiant que notre modèle est capable de définir une règle généralisable. Sur base des données d'entrainement il a été capable de généraliser la règle à n'importe quelle données.

Évaluation d'un apprentissage supervisé

Nous serons confronté à la nécessité d'utilisé et évaluer plusieurs techniques afin de pouvoir identifier celle qui nous permettra d'obtenir le modèle le plus efficient au regard de nos données. Selon la technique, nous serons également amené à évaluer différentes configurations pouvant mener à un meilleur ou moins bon apprentissage.

L'objectif d'un apprentissage supervisé est de créer une règle généralisable. C'est à dire un apprentissage qui sera performant pour de nouvelles données. Deux cas sont à éviter : le sous-apprentissage et le sur-apprentissage. Dans un sous-apprentissage, la machine n'a pas passer les premières épreuves ( validation ) et par conséquent, le modèle est mauvais sur ses données d'apprentissage, et il le sera également pour de nouvelles données. Dans un sur-apprentissage, la machine a réussi avec brio la première épreuve de validation ( même trop bien ! ) mais lorsqu'on la test sur des données que l'on connait, les résultats sont mauvais car elle a trop épousé la forme des données d'apprentissage et ne donne donc pas une règle généralisable.

Nous reprenons en détails ces deux cas ci-dessous.

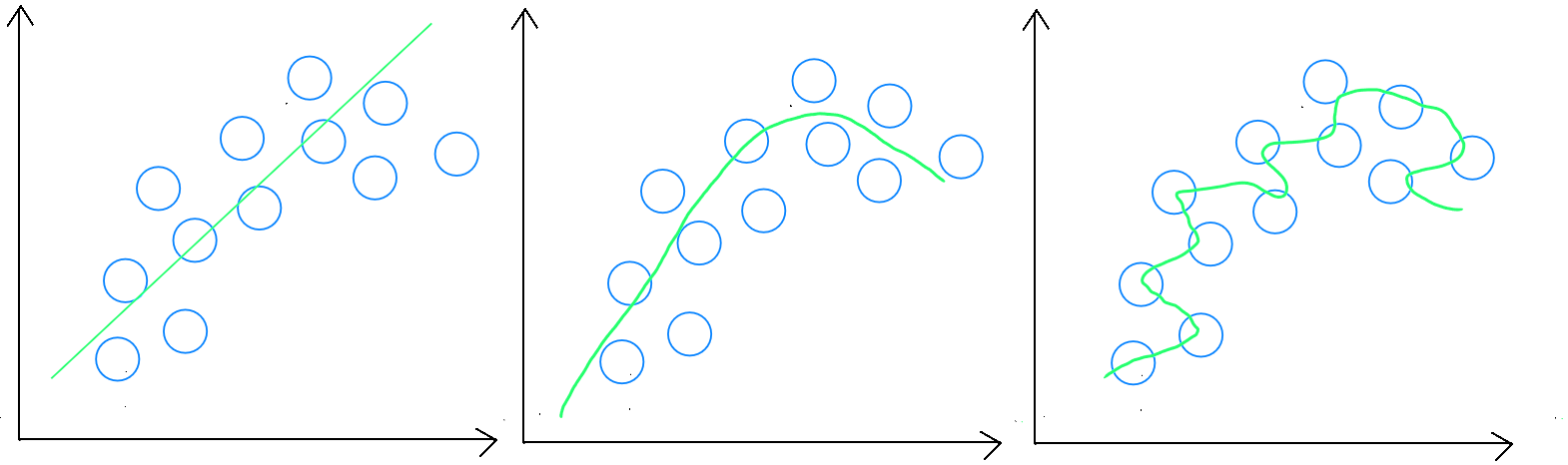
Estimation : sous-apprentissage, règle généralisable et sur-apprentissage

Estimation_Learning

Classement : sous-apprentissage, règle généralisable et sur-apprentissage

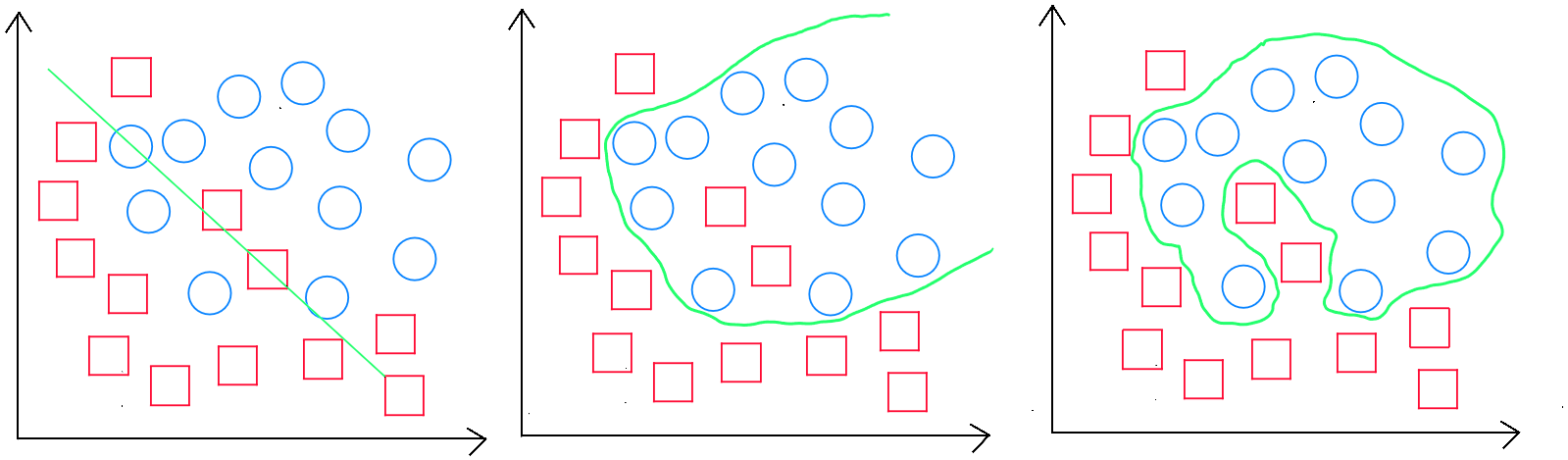
Classement_Learning

Règle généralisable

Les erreurs de prédiction dans le set d’entrainement ( validation ) nous donnent une indication sur l’ajustement du modèle ( sous-entraîné ou surentrainé ). Par exemple, si l’erreur d’entrainement est de 0, mon modèle est certainement en sur-apprentissage, il est en effet impossible d'obtenir un modèle parfait. Les erreurs de prédiction dans le set de validation devraient toutefois être minimisées étant donné que notre modèle a été entrainé sur base de ces données. Si le set de validation présente un taux d'erreur plus important, il est fort probable que nous soyons en sous-apprentissage. Enfin, les erreurs de prédiction dans le set de test ( erreurs prédictives ) mesurent la capacité de prédiction du modèle et devraient être légèrement plus importante que dans le set de validation, sans pour autant s'en écarter de manière trop importante afin de démontrer la capacité du modèle à avoir créé une règle généralisable.

Sous-apprentissage

Le sous-apprentissage apparait lorsque l’échantillon d’apprentissage ne couvre pas suffisamment de cas différents ou les variables sont insuffisantes en termes de quantité, le modèle peut avoir du mal à généraliser correctement. En sous-apprentissage absolu, nous obtiendrons un mauvais résultat lors de l'application de l'étape de validation. Toutefois nous pourrions également rencontrer le cas où l'étape d'apprentissage obtiendrait un score qui paraitrait "bon" mais où l'application du modèle aux données de test renverrait un mauvais score.

Sur-apprentissage

Le sur-apprentissage apparait surtout lorsque l’échantillon est trop important. Pour ajuster son modèle, il faut donc soit diminuer la taille de l’échantillon, soit le augmenter le nombre de variables explicatives. En sur-apprentissage absolu, nous obtenons un excellent résultat lors de l'application de l'étape de mais un mauvais score lors de l'application du modèle aux données de test renverrait un mauvais score.

Évaluation d'un modèle d'estimation

Dans le cadre d'une estimation, les erreurs de prédiction dans le set d’entrainement ( validation ) nous donnent une indication sur l’ajustement du modèle ( sous-entraîné ou surentrainé ). Par exemple, si l’erreur d’entrainement est de 0, mon modèle est certainement en sur-apprentissage. Les erreurs dans le set validation doivent être inférieures aux erreurs dans le set de test étant donné que le modèle a été entrainé sur base du set d’entrainement ( et donc du set de validation ).

Une erreur $(e)$ est en réalité la différence entre la valeur réelle de $y$ et la valeur prédite par le modèle que l'on nomme $\hat{y}$

$e = y-ŷ$ . On notera $e_i = (𝑦_i − ŷ_i )$ pour l'erreur d'un enregistrement spécifique.

attention

Il est important de considérer qu'il existe différents indicateurs d'évaluation et spécifiques selon la technique statistique utilisée.

Dans tous les cas, la littérature privilégie l'utilisation de l'erreur quadratique moyenne ( Mean Square Error - MSE ) ou la racine carrée de l'erreur quadratique moyenne ( Root Mean Square Error - RMSE ) pour l'évaluation d'une estimation :

MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2

Cette formule pourrait également être écrite comme suit :

MSE = \frac{1}{n} \sum_{i=1}^{n} (e_i)^2

Le carré de l'erreur quadratique moyen calcule la moyenne des écarts au carré et est donc plus sensible aux erreurs importantes. Concernant la racine carrée de l'erreur quadratique moyenne ( RMSE ), il se calcule comme suit :

RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}

Cette formule pourrait également être écrite comme suit :

RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (e_i)^2}

où $e_i = y_i - \hat{y}_i$ (l'erreur de chaque enregistrement) et $n =$ le nombre total d'enregistrements.

La racine carrée de l'erreur quadratique moyenne ( RMSE ) est exprimée dans les mêmes unités que les données originales. Si l'on essaie de prédire le prix d'une maison et que l'on obtient un RMSE de 75.000 € et que l'échelle $min/max$ des prix des maisons de votre modèle est de $350.000 € - 500.000 €$ , il va de soi que le RMSE obtenu n'est pas optimal. Par contre si ces mêmes valeurs des maisons de votre modèle sont de $1.950.000 € - 2.550.000 €, un RMSE de 75.000 € est considéré comme faible et donc un bon modèle. L'évaluation du RMSE doit tenir compte de l'échelle des données.

Toutefois, il est important de souligner qu'un des principes de base d'un modèle d'apprentissage est de normaliser ou standardiser les données afin de mettre les données sur une échelle commune et rendre le modèle plus efficient. Par exemple, si nous souhaitons créer un modèle sur l'ensemble de nos données comprenant tant des ventes d'appartements, de maisons que de villa haut de gamme, notre modèle contiendra de nombreux enregistrements améliorant la diversité et donc favorisant une règle généralisable.

Dans ce cas, nous souhaitons obtenir une valeur du RMSE proche de $0$ indiquant un très bon ajustement. Attention toutefois à considérer qu'un RMSE correspondant à $0$ dans la phase de validation ( application du modèle sur les mêmes données que celles à partir desquelles il a été entrainé ), est signe d'un surapprentissage. Ce surapprentissage sera confirmé si en phase de test, le RMSE obtenu est très élevé. Nous souhaitons en effet obtenir un RMSE faible ( très faible ) en validation et en test un RMSE moins performant que la validation mais sans pour autant creuser un écart trop important.

Évaluation d'un modèle de classement

Dans le cadre d'un classement, notre modèle attribuera une classe à la valeur prédite. Prenons le cas d'un modèle de classement à deux classes ( exemple contagieux (1) / non contagieux (0) ). $\hat{y}$ aura donc comme valeur finale possible $1$ ou $0$ . Bien entendu, nous n'obtiendrons pas un modèle parfait. Par conséquent, pour certaines valeurs de $y = 1$ , notre $\hat{y}$ correspondra parfois à $1$ et parfois à $0$ .

Si nous avons plus de deux classes, par exemple Bon, moyen ou mauvais, $\hat{y}$ aura comme valeurs finales possibles $1$ , $2$ ou $3$ et pour certaines valeurs de $y = 1$ , notre $\hat{y}$ correspondra parfois à $1$ , parfois à $2$ et parfois à $3$ .

Pour évaluer un modèle de classement, nous créons une matrice - la matrice de confusion - dans laquelle nous résumons les classements corrects et incorrects. Cette matrice nous permet de calculer le taux de précision et/ou le taux d'erreur global.

Prenons l'exemple d'un modèle dont l'objectif est de prédire pour $\hat{y}$ soit une valeur $1$ soit une valeur $0$ . Dans ce cas, la matrice contiendra 4 cases comme suit :

	Y = 0	Y = 1
ŷ = 0	55	3
ŷ = 1	9	33

Pour calculer le taux de précision, il suffit d'additionner les valeurs évaluées correctement que nous divisons par le total de valeur.

\text{Taux de précision} = \frac{\color{green}{55} + \color{green}{33}}{\color{green}{55} + \color{red}{3} + \color{red}{9} + \color{green}{33}} = \text{88\%}

Pour calculer l' erreur globale, il suffit de soustraire le taux de précision de $1 = 22 \%$

\text{Taux d'erreur globale} = 1 -\text{Taux de précision}

Ce qui nous intéresse, ce sont les prédictions correctement réalisées, à savoir, les vrais négatifs ( les non-contagieux qui sont correctement prédits comme non-contagieux ) et les vrais positifs ( les contagieux qui sont prédits comme contagieux) contrairement aux faux positifs ( les non-contagieux qui sont prédits comme étant contagieux ) et les faux négatifs ( les contagieux qui sont prédits comme non-contagieux ). Le matrice se présente de la manière suivante :

	Y = 0 Non-Contagieux	Y = 1 Contagieux
ŷ = 0	Vrais négatifs	Faux négatifs
ŷ = 1	Faux positifs	Vrais positifs

Dans notre cas, nous avons définis un seuil à $0.5$ , à savoir qu'un résultat $>=0.5$ est considéré comme contagieux et un résultat $<0.5$ est considéré comme non contagieux. Il est évidemment plus prudent d'avoir un modèle qui prédit davantage de personne comme étant contagieuses alors qu'elles ne le sont pas plutôt qu'un modèle qui prédit davantage les personnes contagieuses comme étant non-contagieuses. Nous sommes libre évidemment par prudence de réhausser le seuil par exemple à $0.65$ .

Si l'objectif de notre modèle est de prédire plus de deux classes, par exemple : « Bon », « Moyen », « Mauvais »; dans ce cas, nous ajoutons à notre matrice $n$ colonnes supplémentaires, $n$ étant le nombre de classes à prédire.

	Y = 1 (Bon)	Y = 2 (Moyen)	Y = 3 (Mauvais)
ŷ = 1 (Bon)	Vrais positifs "Bon"	Faux positifs "Bon" & Faux négatifs "Moyen"	Faux positifs "Bon" & Faux négatifs "Mauvais"
ŷ = 2 (Moyen)	Faux positifs "Moyen" & Faux négatifs "Bon"	Vrais positifs "Moyen"	Faux positifs "Moyen" & Faux négatifs "Mauvais"
ŷ = 3 (Mauvais)	Faux positifs "Mauvais" & Faux négatifs "Bon"	Faux positifs "Mauvais" & Faux négatifs "Moyen"	Vrais positifs "Mauvais"

De nouveau, pour calculer le taux de précision, il suffit d'additionner toutes les valeurs correctes et de les diviser par le total d'enregistrements.

Découvrez-en plus sur eaqbe.com :

Découvrez nos solutions RPA et IA : https://www.eaqbe.com/technologie
Transformez vos processus grâce à l'automatisation intelligente alimentée par la RPA et l'IA.
Découvrez nos services de consultance : https://www.eaqbe.com/services
Une consultance sur mesure pour optimiser vos données et vos stratégies décisionnelles.
Explorez nos programmes de formation : https://www.eaqbe.com/formations
Développez votre expertise avec des sessions de formation ciblées.
Rencontrez l'équipe eaqbe : https://www.eaqbe.com/fr/team
Découvrez les personnes qui impulsent l'innovation et l'excellence chez eaqbe.

Déroulement d'un apprentissage supervisé​

Répartition d'un dataframe en variables explicatives et variable cible​

Partitionnement des données​

Étape d'apprentissage​

Étape de validation​

Étape de test​

Évaluation d'un apprentissage supervisé​

Règle généralisable​

Sous-apprentissage​

Sur-apprentissage​

Évaluation d'un modèle d'estimation​

Évaluation d'un modèle de classement​