Détection des anomalies

La technique de détection des anomalies est une technique non supervisée dont l'apprentissage consiste à examiner un ensemble de données considérées comme étant des évènements normaux afin de pouvoir détecter un évènement anormal.

remarque

Certains schémas et concepts présentés ici sont inspirés du cours Machine Learning d'Andrew Ng, programme créé en collaboration entre Stanford university Online Education et DeepLearning.AI disponible sur Coursera. Retrouvez le cours original ici : Machine Learning by Andrew Ng.

Prenons l'exemple d'une usine qui produit des moteurs d'avion, et dont la test final est de faire tourner chaque moteur et mesurer les vibrations et la température.

Nous disposons de deux variables $x$ : $x_1$ chaleur générée et $x_2$ intensité des vibrations et des valeurs pour l'ensemble des tests réalisés sur les moteurs et considérés comme étant normaux.

Nous disposons de valeurs pour un nouvel enregistrement $\textcolor{blue}{x_{test}}$.

l'idée de l'anomalie de détection est de définir si les données du nouveau moteur sont similaires aux données des moteurs précédemment fabriqués ?

Pour la détection d'une anomalie, nous disposons donc de données : $x^{(1)},x^{(2)},...,x^{(n)}$ et notre modèle pourrait être considéré comme la probabilité des nouvelles valeurs d’être existantes dans les données « correctes ».

La détection des anomalies fonctionne sur base du principe de l'approximation de gausse. De manière synthétique, cela sous entends que même si les données ne sont pas parfaitement gaussienne, elles peuvent être approximées par une distribution gaussienne - du moins pour la majorité des enregistrements - et cela signifie que les anomalies sont définies comme des points situés loin de cette majorité.

Distribution gaussienne

Une distribution gaussienne est une distribution dites en forme de cloche, qui est symétrique par rapport à sa moyenne. La moyenne définit le centre de la distribution sur l'axe des abscisse ( où le sommet de la courbe se situe ) et la variance mesure la dispersion des données autour de la moyenne.

Dans une distribution gaussienne, la moyenne correspond au mode et à la médiane ( courbe parfaitement symétrique ).

Comme nous l'abordons dans la partie sur les principes de statistique univariée, la variance est une mesure de la dispersion des valeurs d'une variable. Elle correspond à la moyenne des carrés des écarts à la moyenne et est toujours positive.

La variance se calcule comme suit :

$\sigma^2 = \frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}$.

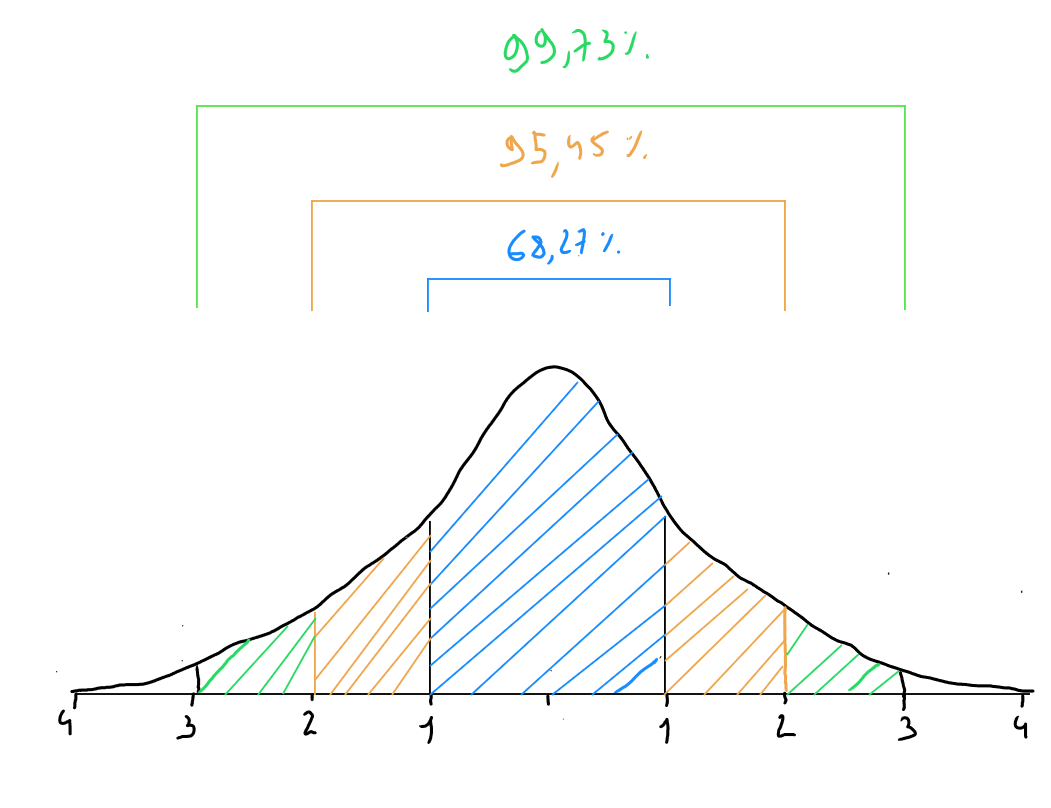
Dans une distribution gaussienne, nous retrouvons la règle empirique suivante :

• $68.27$ des données se trouvent à moins d'un écart-type de la moyenne
• $95.45$ des données se trouvent à moins de deux écarts-types de la moyenne
• $99.73$ des données se trouvent à moins de trois écarts-types de la moyenne

Densité de probabilité d'une distribution normale

La densité de probabilité d'une distribution normale indique la probabilité relative que $X$ prenne une valeur dans une petite intervalle au tour de $x$. Grand $X$ représente tous les résultats possibles d'une variable et petit $x$ est une valeur spécifique que $X$ peut avoir. En d'autres termes : la densité de probabilité indique qu'une valeur aléatoire se situe autour d'une autre valeur.

La formule de la densité de probabilité d'une distribution normale s'écrit comme suit :

$$f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$$

Sachant = $\pi$ correspond à la valeur $3,141592653589793$ et $sigma^2$ à $\frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}$

Nous y retrouvons les propriétés suivantes :

• La somme des probabilités pour toutes les valeurs possibles de $x$ est $100$
• La densité est symétrique autour de la moyenne $μ$. La probabilité est la plus élevée près de $𝜇$ et diminue à mesure que $𝑥$ s'éloigne de $𝜇$
• Les queues de la distribution, qui représentent les événements extrêmes, décroissent très rapidement

Densités de probabilité de $𝑛$ caractéristiques différentes

Dans les cas réel de détection d'anomalie, nous nous retrouvons face à un enregistrement contenant des valeurs pour un ensemble de variables. Il s'agit donc d'une distribution multivariée ( non univariée ). Or, une anomalie peut être un enregistrement dans les valeurs dont certaines variables sont cohérentes à la norme, mais la valeur d'une variable particulière sera anormale. Pour pouvoir identifier cette anormalité, il est important de considérer l'indépendance des caractéristiques et en conséquence de calculer pour chaque variable les densités de probabilité individuelles d'une distribution normal et de les multiplier ensemble par la suite.

Concrètement, cela consisterait à appliquer la formule suivante :

$$p(\mathbf{x}) = p(x_1; \mu_1, \sigma_1^2) \times p(x_2; \mu_2, \sigma_2^2) \times p(x_3; \mu_3, \sigma_3^2) \times \dots \times p(x_n; \mu_n, \sigma_n^2)$$

Cette formule peut être réécrite comme ceci :

$$\prod_{j=1}^{n} \frac{1}{\sqrt{2\pi\sigma_j^2}} \exp\left(-\frac{(x_j - \mu_j)^2}{2\sigma_j^2}\right)$$

Nous disposons de valeurs pour un nouvel enregistrement $\textcolor{blue}{x_{test}}$ auxquelles nous appliquons notre formule.

La règle est la suivante :

• si $\textcolor{blue}{x_{test}}$ < $𝜀$ ( un très petit nombre ) alors
  anormal;
• si $\textcolor{blue}{x_{test}}$ >= $𝜀$ ( un très petit nombre ) alors
  normal;

Nous définissons donc un seuil $𝜀$psylon ( $𝜀$ ) afin de classer un enregistrement comme étant normal ou anormal sur base de la formule de densité de probabilité de $n$ caractéristiques. $𝜀$psylon est un nombre très petit étant donné que nous partons du postulat que $99.73$ des données se trouvent à moins de trois écarts-types de la moyenne.

Définition du seuil $𝜀$psylon

Pour pouvoir définir $𝜀$psylon nous divisons nos données en un set d'entrainement et de validation. Cela fait évidemment penser à une technique supervisées sauf qu'une technique supervisée ne serait pas efficace car dans le cadre de détection d'anomalies, nous disposons en général de « cas » d'anomalies mais ces derniers étant très rares, il est difficile pour un algorithme paramétrique ou non paramétrique de faire une prédiction correcte.

Prenons l'exemple suivant : nous disposons 10.000 enregistrements reprenant des valeurs pour des moteurs d'avions fabriqués et ne présentant aucune anomalie. Nous disposons également de 20 enregistrements ( 20 moteurs ) pour lesquels nous avons constaté une anomalie.

Dans ce cas :

1. Nous divisons les données et nous entrainons notre modèle sur 8.000 enregistrements « normaux ». L'entrainement consister à calculer la densité de probabilité gaussienne pour chaque enregistrement ( $x$ )


2. Nous trions ensuite ces probabilités par ordre décroissant et nous sélectionnons parmi les valeurs les plus faibles, plusieurs valeurs de $p$ ( densité de probabilité gaussienne )


3. Ces valeurs sont testées en tant que seuil $𝜀$ ( $𝜀$psylon ) dans les données de validation 2020 enregistrements restants ( dont 20 sont anormaux ) et on identifie la valeur de $𝜀$ qui définit au mieux les données anormales comme étant anormales sans intégrer de données normales comme étant anormales.

Choix des variables

Nous avons vu jusqu'à présent que notre algorithme réalise les étapes suivantes :

1. Sélection de n caractéristiques : $\vec{x} = [x_1, x_2, ..., x_n]$


2. Calcul des paramètres $\mu_1, ..., \mu_n, \sigma_1^2, ..., \sigma_n^2$


3. Étant donné un nouvel enregistrement pour $x$, calcul de $p(x)$ : $p(x) = \prod_{j=1}^{n} p(x_1 ; \mu_1, \sigma_1^2)$ soit $\prod_{j=1}^{n} \frac{1}{\sqrt{2\pi\sigma}} exp^{-\frac{(x-\mu)^2}{2\sigma^2}}$


4. Résultat = si $p(x) \leq \epsilon$, anomalie ; si $p(x) > \epsilon$, normal

Une des condition sine qua non est de disposer de variables distribuées en forme gaussienne. Cette condition n'est forcément pas toujours remplie et il existe des moyens de renforcer une distribution afin de la rendre gaussienne :

• $np.log(𝑥_1+0.001)$
• $np.log(𝑥_1+1)$
• $np.log(𝑥_1+2)$
• $np.log(𝑥_1+3)$
• $x_1 = \sqrt{x_1}$
• $x_1 = x_1^{1/3}$

Découvrez-en plus sur eaqbe.com :

• Découvrez nos solutions RPA et IA : https://www.eaqbe.com/technologie
  Transformez vos processus grâce à l'automatisation intelligente alimentée par la RPA et l'IA.

• Découvrez nos services de consultance : https://www.eaqbe.com/services
  Une consultance sur mesure pour optimiser vos données et vos stratégies décisionnelles.

• Explorez nos programmes de formation : https://www.eaqbe.com/formations
  Développez votre expertise avec des sessions de formation ciblées.

• Rencontrez l'équipe eaqbe : https://www.eaqbe.com/fr/team
  Découvrez les personnes qui impulsent l'innovation et l'excellence chez eaqbe.

Code Python

import numpy as np
import pandas as pd
from scipy.stats import norm
import matplotlib.pyplot as plt

#Synthetic data
np.random.seed(0)
x1 = np.random.normal(50, 10, 8000)  # 8000 correct records x1  - average 50 ; standard deviation 10
x2 = np.random.normal(30, 5, 8000)   # 8000 correct records x2  - average 30 ; standard deviation 5

# 2000 validation records (1980 normal, 20 not normal)
x1_val = np.random.normal(50, 10, 1980)
x2_val = np.random.normal(30, 5, 1980)

x1_val_anomalous = np.random.normal(80, 5, 20)  
x2_val_anomalous = np.random.normal(10, 5, 20)  

x1_val = np.concatenate([x1_val, x1_val_anomalous])
x2_val = np.concatenate([x2_val, x2_val_anomalous])

train_data = pd.DataFrame({
    'x1': x1,
    'x2': x2
})

val_data = pd.DataFrame({
    'x1': x1_val,
    'x2': x2_val,
    'label': [0]*1980 + [1]*20  # 1 = Anomaly
})

mu_x1, sigma_x1 = np.mean(train_data['x1']), np.std(train_data['x1'])
mu_x2, sigma_x2 = np.mean(train_data['x2']), np.std(train_data['x2'])

def gaussian_probability_density(x, mu, sigma):
    return (1 / (np.sqrt(2 * np.pi) * sigma)) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)


train_data['p_x1'] = gaussian_probability_density(train_data['x1'], mu_x1, sigma_x1)
train_data['p_x2'] = gaussian_probability_density(train_data['x2'], mu_x2, sigma_x2)
train_data['p'] = train_data['p_x1'] * train_data['p_x2']

val_data['p_x1'] = gaussian_probability_density(val_data['x1'], mu_x1, sigma_x1)
val_data['p_x2'] = gaussian_probability_density(val_data['x2'], mu_x2, sigma_x2)
val_data['p'] = val_data['p_x1'] * val_data['p_x2']

epsilons = np.linspace(min(val_data['p']), max(val_data['p']), 1000)
best_epsilon = None
best_f1 = 0

for epsilon in epsilons:
    predictions = val_data['p'] < epsilon
    tp = np.sum((predictions == 1) & (val_data['label'] == 1))
    fp = np.sum((predictions == 1) & (val_data['label'] == 0))
    fn = np.sum((predictions == 0) & (val_data['label'] == 1))

    if tp + fp == 0 or tp + fn == 0:
        continue

    precision = tp / (tp + fp)
    recall = tp / (tp + fn)
    f1 = 2 * precision * recall / (precision + recall)

    if f1 > best_f1:
        best_f1 = f1
        best_epsilon = epsilon

print(f"Best Epsylon found: {best_epsilon}")
print(f"Best F1 Score: {best_f1}")

val_data['anomaly'] = val_data['p'] < best_epsilon

print(f"Detected anomaly: {val_data['anomaly'].sum()} sur {len(val_data)} enregistrements de validation")

plt.figure(figsize=(10, 6))
plt.scatter(val_data['x1'], val_data['x2'], c=val_data['anomaly'], cmap='coolwarm', marker='o')
plt.xlabel('Température (x1)')
plt.ylabel('Vibrations (x2)')
plt.title('Anomalies detection')
plt.show()